앞서 살펴본 TAH 설계 이슈들 참 복잡하죠? 세상에는 공짜가 없습니다. 하나를 얻으려면 하나를 포기해야 하죠. 우리 인생도 만찮가지 입니다. 모든 것을 만족시킬 수 없기 때문에 취사선택 해야 합니다. 그렇다면 취사선택을 어떻게 하면 될까요? 우선순위을 결정하고 중요한 것부터 맞춰나가면 됩니다. 우선순위를 결정하려면 사양 (Specifications) 을 잘 알아야 합니다. 응용분야와 비용에 따라 사양이 결정되고 그 사양에 맟줘 우선순위를 정하게 됩니다. 물론, 경영자들과 마케팅 하시는 분들이 황당한 사양을 요구하는 경우도 있습니다. 모든 것을 만족시키라는 식으로 말이죠. 엔지니어들이 이때 말을 할 수 있어야 합니다. 왜 모든 것을 만족 시킬 수 없는지, 그리고 우선순위에 따라 어떤 것을 취사선택해야 하는지 제시 할 수 있어야 합니다. 그렇게 하기 위해서는 복잡하게 얽혀 있는 관계성을 잘 이해하고 있어야 합니다. 아날로그/혼성모드 회로설계에서는 상당히 중요한 부분이죠.
자, 본론으로 들어가 볼까요. TAH 설계를 시작할 때 가장 중요한 설계 사양은 bandwidth과 noise 입니다. 앞서 설명한 것처럼, 설계 이슈들이 서로 trade-off 관계 (하나를 만족하려면 다른 하나를 포기해야 하는 상황)에 있기 때문에 서로의 연관성을 잘 생각하면서 설계를 시작해야 합니다.
먼저, TAH의 bandwidth를 어떻게 결정하는지 보죠. TAH를 단순히 switch와 C로 구성되어있는 RC LPF 로 생각한다면, bandwidth는 1/(2πRC) 이 되고 입력 아날로그 신호의 최대 주파수를 bandwidth 의 사양으로 결정하면 될 것 같아 보입니다. 예를 들어, 입력 아날로그 신호의 최대 주파수가 500MHz 라고 한다면 ‘bandwidth는 최소 500MHz가 되면 되겠지?’ 라고 생각을 하고 bandwidth = 1/(2πRC) = 500MHz 로 해서 RC = 1/(2π*500M) 로 계산하려 합니다. 하지만, 이렇게 하면 안됩니다. 왜 그럴까요? 그 이유는 TAH의 sampling 동작이 RC 회로의 시상수로 결정이 되기 때문입니다. 좀 더 정확히 말하면 sampling 시간과 그 시간동안 sampling 되어야 하는 아날로그 신호의 목표 값에 의해 결정이 됩니다. 그리고 그 목표값은 ADC의 해상도로 결정이 됩니다. 이렇게 이야기를 하면 당연히 이해가 안되겠죠? 예를 들어보죠.
TAH의 sampling clock 주파수 (MOS switch를 on/off 시키는 클럭 입니다.)가 1GHz고 duty cycle이 50%라고 합시다. 그리고, TAH의 MOS switch로 들어오는 입력 아날로그 신호의 최대 주파수가 500MHz (sampling 주파수1GHz의 절반이죠. 우리는 이것을 Nyquist 주파수라고 합니다.) 라고 합시다. 그리고 SAR ADC의 해상도를 6 bit 이라고 가정하죠. 그렇다면 1GHz sampling clock의 전체 주기는 1nsec 입니다. 그리고 이놈의 duty cycle이 50% 이기 때문에 처음 0.5nsec 동안 (보통 clock이 high 상태인 시간) 은 sampling mode가 되고 나머지 0.5nsec 동안 (보통 clock이 low상태인 시간)은 hold mode 입니다. 따라서, sampling mode인 0.5nsec 동안 입력 아날로그 신호가 정확히 sample 되어야 합니다. 이때, 얼마나 ‘정확히’ 라는 의문이 생기게 됩니다. 예를 들어서, sampling mode 동안 입력되는 아날로그 신호가 1V 라면, 1V의 전압이 순간적으로 C에 저장되지 않고 서서히 저장되면서 1V에 가까워지죠 (이것은 RC 로 구성된 LPF 특성 때문입니다.) 우리에게 주어진 시간이 충분하다면 문제가 없지만 우리에게는 0.5nsec만 있을 뿐입니다. 그렇다면, 0.5nsec 동안 어느 수준까지 C에 충전을 해야 할까요? 0.9V?, 0.95V?, 아니면 0.99V?….. 바로 이 부분에서 ADC의 해상도가 등장 합니다. 보통 ADC 설계에 있어서 TAH의 C에 충전되야 하는 값은 ‘최종값으로 부터 ADC의 0.5 LSB 이내’ 가 되야 합니다. 왜 0.5 LSB냐구요? 이거 설명하려면 또 한참 걸리니까 나중에 다시 자세히 설명할께요. 간단히 설명하면 0.5LSB를 선택하는 이유는, 0.5LSB를 넘어가면 ADC 의 quantization error가 커져서 ADC 성능에 문제가 될 수 있기 때문 입니다. 일단은 ‘ADC의 0.5 LSB 이내’ 라고 외워두세요. 이때, LSB 단위를 사용하는 이유는 입력 아날로그 신호의 최대값을 기반으로 정의하기 때문이죠 (C에 충전되는 시간이 가장 오래 걸릴 때는 입력 아날로그 신호가 최대일 때를 생각하면 이해하 실 수 있습니다.).
정리하면, ‘0.5nsec 안에 최종값으로 부터 ADC의 0.5 LSB 내에서 아날로그 신호를 sampling 해야한다’ 라고 할 수 있습니다. 이제 0.5LSB가 어느정도로 정확한 값인지 살펴보죠. 6b ADC경우는 총 64 (=26) LSB 를 가지는데 이때, 0.5 LSB 는 전체 LSB와 비교했을 때 1/128 (=0.5LSB/64LSB)에 해당합니다. 이것을 퍼센트로 표현하면 (1/128)*100 %= 0.78125% 가 됩니다. 즉, ADC의 0.5 LSB 내에서 sampling 한다는 의미는 이상적인 최종 sampling 값과 비교했을 때 오차가 0.78125% 가 되는 시점까지 sampling 한다는 의미가 됩니다. 자, 그러면 위의 조건을 만족하는 bandwidth와 MOS switch on resistance 그리고 C 값을 계산해보죠.
RC 회로의 입출력 관계식은 Vout (t) = Vin(t)*(1-EXP(-t/RC))에서, 시간 t에서 오차값은EXP(-t/RC) 입니다. (회로망 책을 참조하세요)
그리고 이 오차값이 결국 정확도 (accuracy)를 나타냅니다. 이제 이 오차값을 err 라고 하겠습니다. 이제 Tau = RC 라고 하면, 오차값은 다음과 같이 표현 됩니다.
err = EXP(-t/Tau)
자, 이제 이 식에서 Tau를 구할 겁니다. 잘 보세요. 위 식은 양변에 자연로그를 취해서 정리하면 아래와 같이 됩니다.
t = LN(1/err) * Tau
여기서, m = LN(1/err) 라고 해볼까요? 그러면 식은
t = m * Tau 이 됩니다. 우리는 ‘m’ 을 ‘Tau factor’ 라고 합니다.
주어진 시간과 m을 알수 있으면 우리가 원하는Tau를 구할 수 있습니다. 그리고 이렇게 구해진 Tau 를 가지고 필요한 bandwidth 를 구할 수 있습니다. (BW = 1/(2*pi*Tau)) 그럼, 실제값을 넣어서 한번 계산해 볼까요? 주어진 시간은 얼마였죠? 위에서 설명한 것처럼 한 주기의 절반이었죠? 그러니까, t = 0.5/1GHz = 0.5nsec 입니다.
자, 이번에는 m을 구해보죠. 이상적인 경우라면, err = 0 가 되어야 하고 이렇게 되면 m = LN(1/err) 식에 의해 m 은 무한대값이 되어야 합니다. 하지만, 실제의 경우는 RC 회로의 제한된 bandwidth 때문에 그렇게 되지 못하고 항상 error 값이 존재합니다.
그렇다면 우리에게 주어진 시간 0.5sec에서 얼마의 error 값을 가져야 할까요? 네, 그렇습니다. 위에서 우리가 0.5LSB의 정확도가 필요하다고 했죠? 바로 이 값이 error 가 됩니다 (잘 생각해 보세요). 이제 m을 구할 수 있습니다. 먼저 target error 를 구하면,
err = 1/(2^(N+1)) = 1/(2^7) = 1/128 가 되고, 여기에서 m 을 구하면,
m = LN (1/err) = LN (128) = 4.852
이제, t하고 m을 아니까Tau를 구할 수 있습니다.
Tau = t/m = 0.5n/4.852 = 0.10305nsec 가 됩니다. 그리고 Tau에서 bandwidth를 구하면,
bandwidth = 1/(2π*Tau) = 1/(2π*0.10305n) = 1.54GHz 가 됩니다.
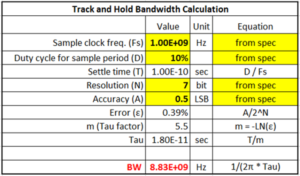
계산이 무지 복잡하죠. 쉽게 외우는 방법을 알려드리겠습니다. 외우는 방법 (순서)는 아래와 같습니다.
- BW = 1/(2π*Tau)
- Tau = Ts/m
- m = -LN(error)
- error = 0.5/2N
- N = number of bit
- Ts = Sampling Time
그리고 계산할 때는 아래에서 위로 역방향으로 계산하면서 올라가면 됩니다. 어디에서 적어서 붙여 놓으세요. 영어 단어 외우듯이 말이죠. 아래 표는 이런 방법으로 계산한 예제 입니다. 엑셀로 간단히 만들수 있습니다. 한번 만들어 보시기 바랍니다.
이제 R 과 C를 결정해 볼까요?
다들 아는 것처럼 R*C (시상수) 가 Tau를 결정하게 되죠. Tau = R*C.
따라서, R 혹은C 중 하나를 결정하면 다른 하나가 결정이 됩니다.
예를 들어서 R=100 ohm 라고 한다면, C= 0.1n/100 = 1pF 가 됩니다.
R 값은 MOS switch의 W/L 값과 VOD (overdrive voltage) 값으로 결정됩니다 (정확하게는 (W/L)*(VOD) 의 역수입니다. 왜 그런지는 MOS 의 deep triode region의 on resistance를 찾아보세요).
그러면 실제 R과 C를 어떻게 결정할까요? 바로 noise 사양에 의해 결정됩니다. RC LPF의 noise power는 R 값에 관계없이 4KT/C 로 결정이 됩니다 (‘Low Pass Filter의 noise가 R에 독립적인 이유’ 참조하세요). 따라서, noise 사양이 결정되면 C 가 결정됩니다 (K와 T는 Kevin 상수와 절대온도 입니다). 일반적으로 ADC 해상도가 커질 수록 noise 사양은 점점 중요해집니다. 왜냐면, 해상도가 커지면 noise 가 신호로 인식될 수 있기 때문이죠. Noise 요구사항으로 C가 결정이 되면 Tau=R*C 에서 R을 결정하면 됩니다. R 이 결정되면 MOS switch의 W/L 이 결정이 되는거죠. 지금까지의 과정을 통하여 R과C가 결정이 됩니다. 하지만, 최종적으로는 simulation을 통하여 검증을 해야 합니다.
정리하겠습니다. TAH를 구성하는 MOS swithc와 C는 sampling 시간과 ADC의 해상도 그리고 noise 사양에 의해 결정이 됩니다. Sampling 시간이 짧아질수록 (= sampling frequecy가 높아질수록), ADC가 고해상도가 될수록, 그리고 low noise 설계를 해야 할 수록 설계는 점점 힘들어 집니다. 높은 주파수와 고해상도에서 TAH를 동작시키려면 bandwidth 를 높여야 하는데 그렇게 하려면 R과 C를 줄여야 하기 때문이죠. R을 줄이려면 MOS switch를 크게해야 합니다. MOS switch를 크게하면 다른 문제들(parasitic capacitance, 전력소모)이 생깁니다. 그리고 C를 작게 하면 noise 가 커집니다. 서로 물고 물려있는 trade-off 입니다.